Question

Be sure to answer all parts. Compare the wavelengths of an electron (mass = 9.11 × 10−31 kg) and a proton (mass = 1.67 × 10−27 kg), each having (a) a speed of 6.66 × 106 m/s and (b) a kinetic energy of 1.71 × 10−15 J.

Answer 1

Step-by-step explanation:

Given that,

(a) Speed,
`v=6.66* 10^6\ m/s`

Mass of the electron,
`m_e=9.11* 10^(-31)\ kg`

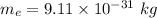
Mass of the proton,
`m_p=1.67* 10^(-27)\ kg`

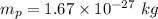
The wavelength of the electron is given by :

`\lambda_e=(h)/(m_ev)`

`\lambda_e=(6.63* 10^(-34))/(9.11* 10^(-31)* 6.66* 10^6)`

`\lambda_e=1.09* 10^(-10)\ m`

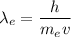
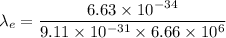
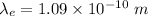
The wavelength of the proton is given by :

`\lambda_p=(h)/(m_p v)`

`\lambda_p=(6.63* 10^(-34))/(1.67* 10^(-27)* 6.66* 10^6)`

`\lambda_p=5.96* 10^(-14)\ m`

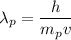
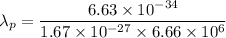
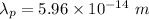
(b) Kinetic energy,
`K=1.71* 10^(-15)\ J`

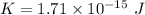
The relation between the kinetic energy and the wavelength is given by :

`\lambda_e=(h)/(√(2m_eK))`

`\lambda_e=\frac{6.63* 10^(-34)}{\sqrt{2* 9.11* 10^(-31)* 1.71* 10^(-15)}}`

`\lambda_e=1.18* 10^(-11)\ m`

`\lambda_p=(h)/(√(2m_pK))`

`\lambda_p=\frac{6.63* 10^(-34)}{\sqrt{2* 1.67* 10^(-27)* 1.71* 10^(-15)}}`

`\lambda_p=2.77* 10^(-13)\ m`

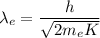
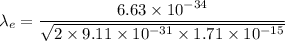
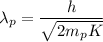
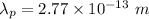
Hence, this is the required solution.