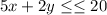Question

Find the solution of the objective function for problems (a) - (b) below. For each problem,

confirm that the optimum satisfies the Kuhn-Tucker conditions. At each solution, describe
whether the constraint(s) is binding.
a) Minimize the function
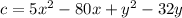
`c = 5x^(2) - 80x + y^(2) - 32y` subject to the constraints
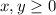
`x,y\geq 0` and

`x+y\geq 20`
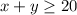
b) Maximize the profit function
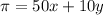
`\pi = 50x +10y` subject to the constraints
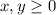
`x,y \geq 0` and
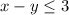
`x-y\leq 3` and
`5x+2y\leq \leq 20`

Answer 1

is that all detail

Explanation: