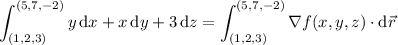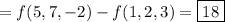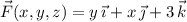
is conservative if there is a scalar function
 such that
such that
 . This would require
. This would require
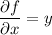
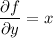
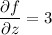
(or perhaps the last partial derivative should be 4 to match up with the integral?)
From these equations we find
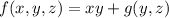
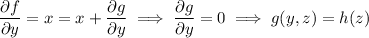
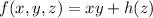
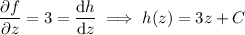

so
 is indeed conservative, and the gradient theorem (a.k.a. fundamental theorem of calculus for line integrals) applies. The value of the line integral depends only the endpoints:
is indeed conservative, and the gradient theorem (a.k.a. fundamental theorem of calculus for line integrals) applies. The value of the line integral depends only the endpoints: