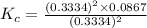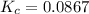Question

At a certain temperature, 0.760 mol SO3 is placed in a 1.50 L container. 2SO3(g) = 2SO2(g) + O2(g)At equilibrium, 0.130 mol O2 is present. Calculate Kc.

Answer 1

`K_c=0.0867`

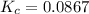
Step-by-step explanation:

Moles of SO₃ = 0.760 mol

Volume = 1.50 L

`Molarity=(Moles\ of\ solute)/(Volume\ of\ the\ solution)`

`Molarity=(0.760)/(1.50\ L)`

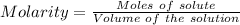
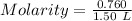
[SO₃] = 0.5067 M

Considering the ICE table for the equilibrium as:

Given:

Equilibrium concentration of O₂ = 0.130 mol

Volume = 1.50 L

`Molarity=(Moles\ of\ solute)/(Volume\ of\ the\ solution)`

`Molarity=(0.130)/(1.50\ L)`

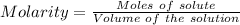
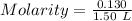
[O₂] = x = 0.0867 M

[SO₂] = 2x = 0.1733 M

[SO₃] = 0.5067-2x = 0.3334 M

The expression for the equilibrium constant is:

`K_c=\frac {[SO_2]^2[O_2]}{[SO_3]^2}`

`K_c=((0.3334)^2* 0.0867)/((0.3334)^2)`

`K_c=0.0867`