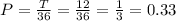Answer:
0.33
Explanation:
Two fair number cubes can be thought as dice with sides numbered from 1 to 6. The throw of two dice may result in one of the following combinations in which (d1,d2) are the results of die 1 and 2 respectively:
Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
There are 36 as many possible combinations
The sum of both quantities will produce 11 possible results
S={2,3,4,5,6,7,8,9,10,11,12}
The combinations which produce a sum of 4 are (1,3)(2,2),(3,1), 3 in total
The combinations which produce a sum of 5 are (1,4)(2,3),(3,2),(4,1) 4 in total
The combinations which produce a sum of 6 are (1,5)(2,4),(3,3),(4,2),(5,1) 5 in total
If we want to know the probability that the sum of the results of the throw is 4,5, or 6, we compute the total ways to produce them
T=3+4+5=12 combinations
The probability is finally computed as