To solve the problem it is necessary to apply the concepts related to heat flow,
The heat flux can be defined as

Where,
k = Thermal conductivity
A = Area of cross-sectional area
d = Length of the rod
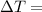 Temperature difference between the ends of the rod
Temperature difference between the ends of the rod
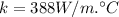 Thermal conductivity of copper rod
Thermal conductivity of copper rod
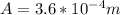 Area of cross section of rod
Area of cross section of rod
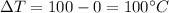 Temperature difference
Temperature difference
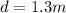 length of rod
length of rod
Replacing then,
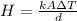
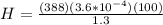
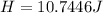
From the definition of heat flow we know that this is also equivalent
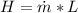
Where,
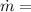 Mass per second
Mass per second
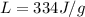 Latent heat of fusion of ice
Latent heat of fusion of ice
Re-arrange to find
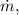
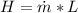
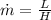
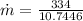
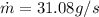
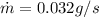
Therefore the mass of ice per second that melts is 0.032g