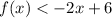Question

Question 4 Multiple Choice Worth 1 points)

(04.06 MC)
In the graph, the area below f(x) is shaded and labeled A, the area below g(x) is shaded and labeled B, and the area where f(x) and g(x) have shading in
common is labeled AB.
9
.
The graph represents which system of inequalities?

Answer 1

`f(x)<-2x+6`

`g(x) \leq x+2`

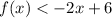
Explanation:

step 1

Fin the equation of the linear inequality f(x)

we know that

The solution of the linear inequality f(x) is the shaded area below the dashed line

The y-intercept of the dashed line is (0,6)

The x-intercept of the dashed line is (3,0)

The slope of the dashed line is negative and its value is equal to

`m=(0-6)\(3-0)=-2`

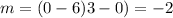
The linear function f(x) in slope intercept form is equal to

`f(x)=-2x+6`

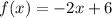
therefore

The linear inequality f(x) is equal to

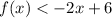`f(x)<-2x+6` ----> is < because is a dashed line and the shaded area is below the line

step 2

Fin the equation of the linear inequality g(x)

we know that

The solution of the linear inequality g(x) is the shaded area below the solid line

The y-intercept of the solid line is (0,2)

The x-intercept of the solid line is (-2,0)

The slope of the solid line is positive and its value is equal to

`m=(0-2)\(-2-0)=1`

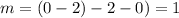
The linear function g(x) in slope intercept form is equal to

`g(x)=x+2`

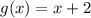
therefore

The linear inequality g(x) is equal to

`g(x) \leq x+2` ----> is ≤ because is a solid line and the shaded area is below the line

therefore

The system of inequalities is equal to

`f(x)<-2x+6`

`g(x) \leq x+2`