Question

An atom of 206Pb has a mass of 205.974440 amu. Calculate its binding energy in MeV per nucleon.

Use the masses:mass of 1H atom = 1.007825 amu mass of a neutron = 1.008665 amu 1 amu = 931.5 MeV

Answer 1

Answer: The binding energy of the given nucleus is 7.88 MeV/nucleon

Step-by-step explanation:

Nucleons are defined as the sub-atomic particles which are present in the nucleus of an atom. Nucleons are protons and neutrons.

We are given a nucleus having representation:
`_(82)^(206)\textrm{Pb}`

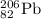
Number of protons = 82

Number of neutrons = 206 - 82 = 124

To calculate the mass defect of the nucleus, we use the equation:

`\Delta m=[(n_p* m_p)+(n_n* m_n)-M`

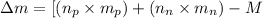
where,

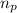`n_p` = number of protons = 82

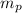`m_p` = mass of one proton = 1.007825 amu

`n_n` = number of neutrons = 124

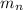`m_n` = mass of one neutron = 1.008665 amu

M = nuclear mass = 205.974440 amu

Putting values in above equation, we get:

`\Delta m=[(82* 1.007825)+(124* 1.008665)]-205.974440\\\\\Delta m=1.74167amu`

To calculate the binding energy of the nucleus, we use the equation:

`E=\Delta mc^2\\E=(1.74167u)* c^2`

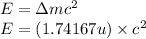
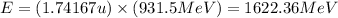`E=(1.74167u)* (931.5MeV)=1622.36MeV` (Conversion factor:
`1u=931.5MeV/c^2` )

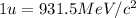Number of nucleons in
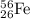`_(26)^(56)\textrm{Fe}` atom = 206

To calculate the binding energy per nucleon, we divide the binding energy by the number of nucleons, we get:

`\text{Binding energy per nucleon}=\frac{\text{Binding energy}}{\text{Nucleons}}`

`\text{Binding energy per nucleon}=(1622.36MeV)/(206)=7.88MeV/nucleon`

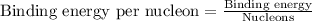
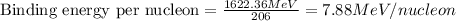
Hence, the binding energy of the given nucleus is 7.88 MeV/nucleon