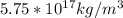Question

calculate the density of a neutron star with a radius 1.05 x10^4 m, assuming the mass is distributed uniformly. Treat the neutron star as a giant ucleaus and consider the mass of a nucleon 1.675 x 10^-27 kg. Your answer should be in the form of N x 10^17 kg/m^3. Enter onlt the number N with teo decimal places, do not enter unit.

Answer 1

To develop this problem it is necessary to apply the concepts related to the proportion of a neutron star referring to the sun and density as a function of mass and volume.

Mathematically it can be expressed as

`\rho = (m)/(V)`

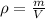
Where

m = Mass (Neutron at this case)

V = Volume

The mass of the neutron star is 1.4times to that of the mass of the sun

The volume of a sphere is determined by the equation

`V = (4)/(3)\pi R^3`

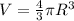
Replacing at the equation we have that

`\rho = (1.4m_(sun))/((4)/(3)\pi R^3)`

`\rho = (1.4(1.989*10^(30)))/((4)/(3)\pi (1.05*10^4)^3)`

`\rho = 5.75*10^(17)kg/m^3`

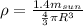
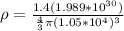
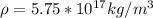
Therefore the density of a neutron star is
`5.75*10^(17)kg/m^3`