2.
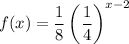
Domain:
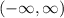 , because any value of
, because any value of
 is allowed and gives a number
is allowed and gives a number
 .
.
Range:
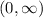 , because
, because
 for any positive real
for any positive real
 .
.
y-intercept: This is a point of the form
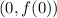 . So plug in
. So plug in
 ; we get
; we get
 . So the intercept is (0, 2), or just 2. (Interestingly, you didn't get marked wrong for that...)
. So the intercept is (0, 2), or just 2. (Interestingly, you didn't get marked wrong for that...)
Asymptote: This can be deduced from the range; the asymptote is the line
 .
.
Increasing interval: Going from left to right, there is no interval on which
 is increasing, since 1/4 is between 0 and 1.
is increasing, since 1/4 is between 0 and 1.
Decreasing interval: Same as the domain;
 is decreasing over the entire real line.
is decreasing over the entire real line.
End behavior: The range tells you
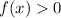 , and you know
, and you know
 is decreasing over its entire domain. This means that
is decreasing over its entire domain. This means that
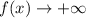 as
as
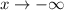 , and
, and
 and
and
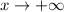 .
.
3.
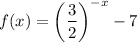
Domain: Same as (2),
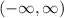 .
.
Range: We can rewrite
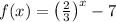 .
.
 for all
for all
 , so
, so
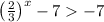 for all
for all
 . Then the range is
. Then the range is
 .
.
y-intercept: We have
 , so the intercept is (0, -6) (or just -6).
, so the intercept is (0, -6) (or just -6).
Asymptote:
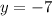
Increasing interval: Not increasing anywhere
Decreasing interval:
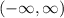
End behavior: Similar to (2), but this time
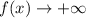 as
as
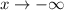 and
and
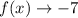 as
as
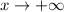 .
.