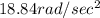Question

A 0.18-kg turntable of radius 0.32 m spins about a vertical axis through its center. A constant rotational acceleration causes the turntable to accelerate from 0 to 24 revolutions per second in 8.0 s.Calculate the rotational acceleration.

Answer 1

Angular acceleration will be
`18.84rad/sec^2`

Step-by-step explanation:

We have given that mass m = 0.18 kg

Radius r = 0.32 m

Initial angular velocity
`\omega _i=0rev/sec`

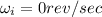
And final angular velocity
`\omega _f=24rev/sec`

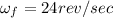
Time is given as t = 8 sec

From equation of motion

We know that
`\omega _f=\omega _i+\alpha t`

`24=0+\alpha * 8`

`\alpha =3rev/sec^2=3* 2* \pi rad/sec^2=18.84rad/sec^2`

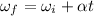
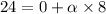
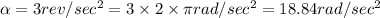
So angular acceleration will be
`18.84rad/sec^2`