Answer:
The acceleration of the rocket while the engine is working is 5 meters per square seconds.
Step-by-step explanation:
Since the rocket accelerates uniformly, the velocity increases linearly and the acceleration (
 ), measured in meters per second, can be determined by definition of secant line:
), measured in meters per second, can be determined by definition of secant line:
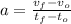 (1)
(1)
Where:
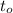 ,
,
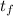 - Initial and final instants, measured in seconds.
- Initial and final instants, measured in seconds.
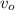 ,
,
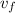 - Initial and final velocities, measured in meters per second.
- Initial and final velocities, measured in meters per second.
If we know that
 ,
,
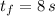 ,
,
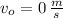 and
and
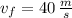 , then the acceleration of the rocket while the engine is working:
, then the acceleration of the rocket while the engine is working:
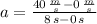
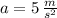
The acceleration of the rocket while the engine is working is 5 meters per square seconds.