Question

A potter's wheel (a solid, uniform disk) of mass 7.0 kg and .65 m radius spins about its central axis. A 2.1 kg lump of clay is dropped onto the wheel at a distance .41 m from the axis. Calculate the rotational inertia of the system.

a. 2.5 kg · m2
b. 1.8 kg · m2
c. 1.5 kg · m2
d. 0.40 kg · m2

Answer 1

The rotational inertia of the system is 1.8 kg.m².

(b) is correct option.

Step-by-step explanation:

Given that,

Mass of disk = 7.0 kg

Radius = 0.65 m

Mass of clay = 2.1 kg

Distance = 0.41 m

We need to calculate the rotational inertia of the system

Using formula of rotational inertia

`I''=I+I'`

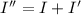
Where, I= the moment of inertia of a solid disk

I'=the moment of inertia of lump of clay

Put the value into the formula

`I=(MR^2)/(2)+mr^2`

`I=(1)/(2)*7.0*(0.65)^2+2.1*0.41^2`

`I=1.8\ kg.m^2`

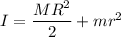
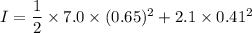
Hence, The rotational inertia of the system is 1.8 kg.m².