Question

The Greater Pittsburgh Area Chamber of Commerce wants to estimate the mean time workers who are employed in the downtown area spend getting to work. A sample of the 15 workers reveals the following number of minutes spent traveling. 29 38 38 33 38 21 45 34 40 37 37 42 30 29 35Develop a 98 percent confidence interval for the population mean. Interpret the results.

Answer 1

98% Confidence interval: (31.74,38.4)

Explanation:

We are given the following data set:

29, 38, 38, 33, 38, 21, 45, 34, 40, 37, 37, 42, 30, 29, 35

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(526)/(15) = 35.07`

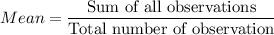
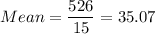
Sum of squares of differences = 506.93

`S.D = \sqrt{\displaystyle(506.93)/(14)} = 6.02`

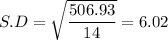
98% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

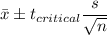
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 14 and}~\alpha_(0.02) = \pm 2.145`

`35.07 \pm 2.145((6.02)/(√(15)) ) = 35.07 \pm 3.33 = (31.74,38.4)`

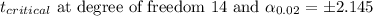
Thus, there is 98% confidence that the population mean number of minutes spent traveling by workers is between 31.74 mins and 38.40