Answer: It is believed that exactly 20% of Evergreen Valley college students attended the opening night midnight showing of the latest harry potter movie.
Explanation:
Since we have given that
n = 84
x = 11
So,
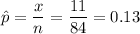
p = 0.20
So, hypothesis:
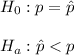
so, test statistic value would be

At 1% level of significance, critical value would be
z= 2.58
Since 2.58>-1.604
So, We will accept the null hypothesis.
Hence, It is believed that exactly 20% of Evergreen Valley college students attended the opening night midnight showing of the latest harry potter movie.