Question

A string that is 3.6 m long is tied between two posts and plucked. The string produces a wave that has a frequency of 320 Hz and travels with a speed of 192 m/s. How many full wavelengths of the wave fit on the string?

Answer 1

To solve this problem it is necessary to apply the concepts related to wavelength depending on the frequency and speed. Mathematically, the wavelength can be expressed as

`\lambda = (v)/(f)`

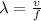
Where,

v = Velocity

f = Frequency,

Our values are given as

L = 3.6m

v= 192m/s

f= 320Hz

Replacing we have that

`\lambda = (192)/(320)`

`\lambda = 0.6m`

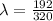
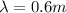
The total number of 'wavelengths' that will be in the string will be subject to the total length over the size of each of these undulations, that is,

`N = (L)/(\lambda)`

`N = (3.6)/(0.6)`

`N = 6`

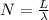
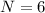
Therefore the number of wavelengths of the wave fit on the string is 6.