Answer:
(3 + 4x)(9 - 12x + 16x²) = 0
(4m - 1)(16m² + 4m + 1) = 0
Explanation:
Here we have to solve the sum of two cubes which is
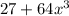
Now, the equation is
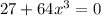
⇒ 3³ + (4x)³ = 0
⇒ (3 + 4x)[3² - 3(4x) + (4x)²] = 0
⇒ (3 + 4x)(9 - 12x + 16x²) = 0
So, (3 + 4x) = 0 or (9 - 12x + 16x²) = 0
Therefore, from the above two relation we can solve for x.
One root will be
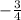 and the others we will get by applying Sridhar Acharya Formula, which will give a pair of conjugate imaginary roots of the equation.
and the others we will get by applying Sridhar Acharya Formula, which will give a pair of conjugate imaginary roots of the equation.
Again, we have to solve the difference of two cubes which is
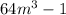
Now, the equation is
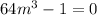
⇒ (4m)³ - 1³ = 0
⇒ (4m - 1)[(4m)² + 4m(1) + 1²] = 0
⇒ (4m - 1)(16m² + 4m + 1) = 0
So, (4m - 1) = 0 or (16m² + 4m + 1) = 0
Therefore, from the above two relation we can solve for m.
One root will be
 and the others we will get by applying Sridhar Acharya Formula, which will give a pair of conjugate imaginary roots of the equation. (Answer)
and the others we will get by applying Sridhar Acharya Formula, which will give a pair of conjugate imaginary roots of the equation. (Answer)