Question

A small town has 2100 inhabitants. At 8 AM, 80 people have heard a rumor. By noon half the town has heard it. At what time will 90% of the population have heard the rumor? (Do not round k in your calculation. Round the final answer to one decimal place.) hours after the beginning

Answer 1

2.7 PM

Explanation:

Since, the rate of spread is proportional to the product of fraction y of people who have heard the rumour and the fraction who have not heard,

`(dy)/(dt)=ky(1-y)`

`(dy)/(y(1-y))=kdt`

`((1)/(y)+(1)/(1-y))dy = kdt`

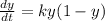
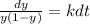
Integrating both sides,

`\int ((1)/(y)+(1)/(1-y))dy = \int kdt`

`\ln y - \ln (1-y) = kt + C`

`\ln ((y)/(1-y)) = kt + C`

`(y)/(1-y)=e^(kt + C)`

`y = e^(kt+C) - y e^(kt+C)`

`y(1+e^(kt+C)) = e^(kt+C)`

`y = (e^(kt+C))/(1+e^(kt+C))`

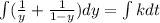
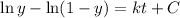
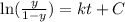
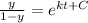
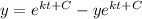
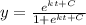
If t = 0, ( at 8 AM ), y =
`(80)/(2100)`

`(80)/(2100)= (e^(0+C))/(1+e^(0+C))`

`(4)/(105)=(e^C)/(1+e^C)`

`4 + 4e^C = 105e^C`

`4 = 101e^C`

`\implies e^C=(4)/(101)`

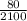
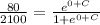
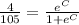
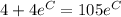
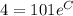
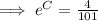
Now, at noon, i.e t = 4, y =
`(1)/(2)`

`(1)/(2)=(e^(4k).(4)/(101))/(1+e^(4k).(4)/(101))`

`(1)/(2)=(4e^(4k))/(101+4e^(4k))`

`101 + 4e^(4k)=8 e^(4k)`

`101 = 4e^(4k)`

`(101)/(4)=e^(4k)`

`((101)/(4))^(1)/(4) = e^k`

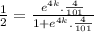
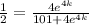
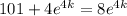
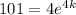
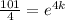
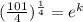
If
`y = (90)/(100)=(9)/(10)`

`(9)/(10)= (((101)/(4))^(t)/(4)* (4)/(101))/(1+((101)/(4))^(t)/(4)* (4)/(101))`

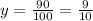
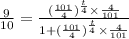
Using graphing calculator,

t ≈ 6.722,

Hence, after 6.722 hours since 8 AM, i.e. on 2.7 PM ( approx ) the 90% of the population have heard the rumour.