Answer:
r = 0.31 m
Step-by-step explanation:
Given that,
Mass of the sculpture, m = 191 kg
The sculpture's moment of inertia with respect to the pivot is,
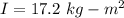
Frequency of oscillation, f = 0.925 Hz
Let r is the distance of the the pivot from the sculpture's center of mass. The frequency of oscillation is given by :
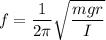
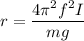
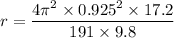
r = 0.31 m
So, the pivot is 0.31 meters from the sculpture's center of mass. Hence, this is the required solution.