Answer: Our required probability is 0.91.
Explanation:
Since we have given that
n = 85
mean = 100 points
standard deviation = 11
We need to find the probability that the sample mean will not differ from the population mean by more than 2 points.
so, it becomes,
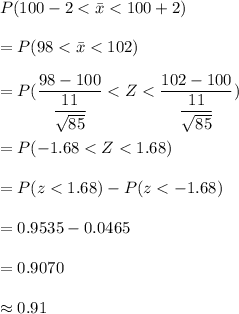
Hence, our required probability is 0.91.