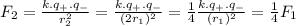Question

According to Coulomb's Law, how does the force between a hydrogen nucleus and an electron in the n =2 level compare with that for one in the n = 1 level if the distance between the nucleus and the n = 2 level is twice as great as that between the nucleus and the n = 1 level?

one-quarter as strong
four times as strong
one-half as strong
twice as strong

Answer 1

one-quarter as strong

Step-by-step explanation:

Coulomb's law gives the mathematical expression to calculate the electrical force (F) between the charge of the nucleus (q₊) and the charge of an electron (q₋) separated by a distance (r).

`F=(k.q_(+).q_(-))/(r^(2) )`

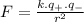
where,

k is the Coulomb's constant

The force between the nucleus and an electron in the level 1 is:

`F_(1)=(k.q_(+).q_(-))/(r_(1)^(2) )`

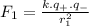
Considering the distance to an electron from n = 2 is twice as great as the distance to an electron from n = 1, the force between the nucleus and an electron in the level 2 is:

`F_(2)=(k.q_(+).q_(-))/(r_(2)^(2) )=(k.q_(+).q_(-))/((2r_(1))^(2) )=(1)/(4) (k.q_(+).q_(-))/((r_(1))^(2) )=(1)/(4)F_(1)`