Answer:
New time period,
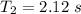
Step-by-step explanation:
Given that,
Mass of the object 1,
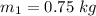
Time period,
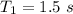
If object 1 is replaced by object 2,

Let
 is the new period of oscillation.
is the new period of oscillation.
The time period of oscillation of mass 1 is given by :
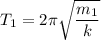
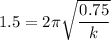 ............(1)
............(1)
The time period of oscillation of mass 2 is given by :
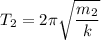
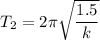 ............(2)
............(2)
From equation (1) and (2) we get :

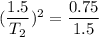
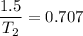
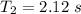
So, the new period of oscillation is 2.12 seconds. Hence, this is the required solution.