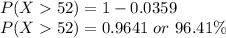Question

A professor's son, having made the wise decision to drop out of college, has been finding his way in life taking one job or another, leaving when his creativity is overly stifled or the employer tires of his creativity. The professor dutifully logs the duration of his son's last few careers and has determined that the average duration is normally distributed with a mean of eighty-eight weeks and a standard deviation of twenty weeks. The next career begins on Monday; what is the likelihood that it endures for more than one year?

Answer 1

0.9641 or 96.41%

Explanation:

Answer 2

0.9641 or 96.41%

Explanation:

Mean career duration (μ) = 88 weeks

Standard deviation (σ) = 20

The z-score for any given career duration 'X' is defined as:

`z=(X-\mu)/(\sigma)`

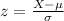
In this problem, we want to know what is the probability that the professor's son's next career lasts more than a year. Assuming that a year has 52 weeks, the equivalent z-score for a 1-year career is:

`z=(52-88)/(20)\\z=-1.8\\`

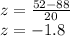
According to a z-score table, a z-score of -1.8 is at the 3.59-th percentile, therefore, the likelihood that this career lasts more than a year is given by:

`P(X>52) = 1-0.0359\\P(X>52) = 0.9641\ or\ 96.41\%`