Question

A disc on a frictionless axle, starting from rest (0 rpm) can spin up to a rotation rate of 3820 rpm in a period of 2 seconds. (This is equivalent to angular acceleration of 200 rad/s.) Moment of inertia of disc = 5 kg-m. a) How much net torque was applied to the disc during the 2-s period? Answer: b) How much net torque would be needed to change the angular acceleration to 400 rad/s"? Answer: c) If the angular acceleration is 400 rad/s, how long will it take to spin up from 0 to 3820 rpm? Answer:

Answer 1

1000 Nm

2000 Nm

1.00007 seconds

Step-by-step explanation:

I = Moment of inertia = 5 kgm²

`\alpha` = Angular acceleration

`\omega_f` = Final angular velocity

`\omega_i` = Initial angular velocity

t = Time taken

Torque is given by

`\tau=I\alpha\\\Rightarrow \tau=5* 200\\\Rightarrow \tau=1000\ Nm`

The torque of the disc would be 1000 Nm

If
`\alpha=400\ rad/s^2`

`\tau=I\alpha\\\Rightarrow \tau=5* 400\\\Rightarrow \tau=2000\ Nm`

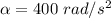
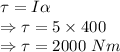
The torque of the disc would be 2000 Nm

From equation of rotational motion

`\omega_f=\omega_i+\alpha t\\\Rightarrow t=(\omega_f-\omega_i)/(\alpha)\\\Rightarrow t=(3820* (2\pi)/(60)-0)/(400)\\\Rightarrow t=1.00007\ s`

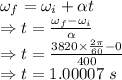
It would take 1.00007 seconds to reach 3820 rpm