Question

Look at the graph of this system of equations: y = - x2 + 1 and y = x2. At which approximate points are the two equations equal? There more than one answer.

A.(-0.7, 0.5)
B.(0.5, 0.7)
C.(0.7, 0.5)
D.(-0.5, 0.7)

Answer 1

option A and C, (-0.7, 0.5) and (0.7, 0.5)

Explanation:

The two equations are equal means, the points at which the two graphs meet.

In that case the x and y coordinates satisfy both the graphs.

let the coordinates at the intersection point be (a,b).

Inserting in first equation,

`b = -a^(2) + 1`

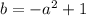
Inserting in second equation,

`b = a^(2)`

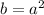
Inserting value of b from second to first equation, we get

`b = -b + 1`

`b = (1)/(2) = 0.5`

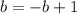
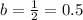
Now inserting the value of b second equation, we get

`(1)/(2) = x^(2)`

`x = \sqrt{(1)/(2) } = +(1)/(1.414) or -(1)/(1.414)  = +0.7  or  -0.7`

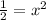
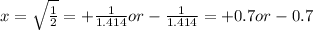
Thus points are, (-0.7, 0.5) and (0.7, 0.5)