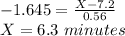Question

A running shoe company wants to sponsor the fastest 5% of runners. You know that in this race, the running times are normally distributed with a mean of 7.2 minutes and a standard deviation of 0.56 minutes.

How fast would you need to run to be sponsored by the company?

a) 6.3 minutes

b) 6.1 minutes

c) 8.3 minutes

d) 8.1 minutes

Answer 1

a) 6.3 minutes

Explanation:

Population mean (μ) = 7.2 minutes

Standard deviation (σ) = 0.56 minutes

The z-score for any running time 'X' is given by:

`z=(X-\mu)/(\sigma)`

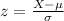
In this scenario, the company is looking for the top 5% runners, that is, runners at and below the 5-th percentile of the normal distribution. The equivalent z-score for the 5-th percentile is 1.645.

Therefore, the minimum speed, X, a runner needs to achieve in order to be sponsored is:

`-1.645=(X-7.2)/(0.56)\\X= 6.3\ minutes`