Question

A random sample of 300 CitiBank VISA cardholder accounts indicated a sample mean debt of 1,220 with a sample standard deviation of 840. Construct a 95 percent confidence interval estimate of the average debt of all cardholders.

Answer 1

Answer: (1124.5619, 1315.4381)

Explanation:

The confidence interval for population mean
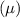`(\mu)` when populatin standard deviation is unknown :-

`\overline{x}\pm t^*(s)/(√(n))`

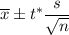
, where
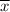`\overline{x}` = Sample mean

`s` =Sample standard deviation

t* = Critical t-value.

Given : n= 300

Degree of freedom : df = n-1 = 299

`\overline{x}=1220`

`s=840`

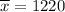
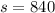
Confidence interval = 95%

Significance level :
`\alpha=1-0.95=0.05`

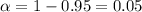
Using t-distribution table ,

The critical value for 95% Confidence interval for significance level 0.05 and df = 299 :
`t^*=t_(\alpha/2,\ df)=t_(0.025,\ 299)=1.9679`

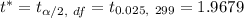
Then, a 95% confidence interval estimate of the average debt of all cardholders will be :-

`1220\pm (1.9679)(840)/(√(300))`

`=1220\pm (1.9679)(840)/(17.3205080757)`

`=1220\pm (1.9679)(48.4974226119)`

`\approx1220\pm 95.4381=(1220-95.438,\ 1220+95.438)\\\\=(1124.5619,\ 1315.4381)`

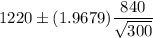
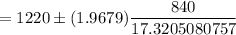
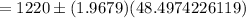
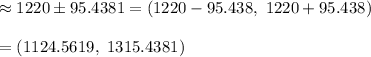
Hence, a 95% confidence interval estimate of the average debt of all cardholders is (1124.5619, 1315.4381) .