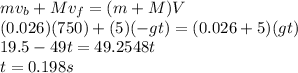Answer:
0.198 s
Step-by-step explanation:
Consider the motion of the block before collision
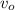 = initial velocity of block as it is dropped = 0 m/s
= initial velocity of block as it is dropped = 0 m/s
 = acceleration = - g
= acceleration = - g
 = time of travel
= time of travel
 = final velocity of block before collision
= final velocity of block before collision
Using the kinematics equation
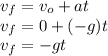
 = mass of the bullet = 0.026 kg
= mass of the bullet = 0.026 kg
 = velocity of block just before collision = 750 m/s
= velocity of block just before collision = 750 m/s
 = mass of the block = 5 kg
= mass of the block = 5 kg
 = final velocity of bullet block after collision = gt
= final velocity of bullet block after collision = gt
Using conservation of momentum