Question

A 15-cm-tall closed container holds a sample of polluted air containing many spherical particles with a diameter of 2.5 μm and a mass of 1.9 x 10^−14 kg. How long does it take for all of the particles to settle to the bottom of the container?

Answer 1

The time it takes for all the particles to settle to the bottom of the container is approximately 17.4 hours.

To calculate how long it takes for all the spherical particles to settle to the bottom of the container, we need to consider the motion of these particles in a viscous medium.

The motion of a particle in a viscous medium is described by Stokes' law, which states that the drag force on a particle is given by D = 6πηrv, where η is the viscosity of the medium, r is the radius of the particle, and v is the velocity of the particle.

Assuming the air in the container is at room temperature (about 25°C) and atmospheric pressure, we can use the dynamic viscosity of air at this temperature, which is approximately
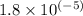`1.8 * 10^((-5))` Pa.s or kg/m.s.

The radius of the particle is half the diameter, so r =
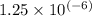`1.25 * 10^{(-6)` m.

The settling velocity of a particle is the velocity at which the drag force is equal to the gravitational force.

We can calculate this velocity using the equation D = mg, where m is the mass of the particle and g is the acceleration due to gravity.

Plugging in the values, we have D = 6π(
`1.8 * 10^((-5))` )(
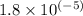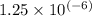`1.25 * 10^{(-6)` )v =
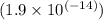`(1.9 * 10^((-14)))`(9.8)

Solving for v gives v ≈
`2.39 * 10^{(-6)` m/s.

To find the time it takes for all the particles to settle, we need to divide the height of the container by the settling velocity.

The height of the container is 15 cm, which is 0.15 m.

Therefore, the time it takes for all the particles to settle is t =
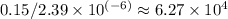`0.15/2.39 * 10^((-6)) \approx 6.27 * 10^4` s, or about 17.4 hours.