Question

Which answer choice is a solution to the inequality 1.5x + 3.75 greater than or equal to 5.5

Answer 1

`x` ≥
`(7)/(6)`

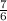
Explanation:

The expression we have is:

`1.5x+3.75` ≥
`5.5`

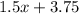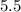
To find the solution of x, we need to clear the inequality until we leave the x on one side.

For this, the first step is to move 3.77 to the left with a minus sign:

`1.5x` ≥
`5.5-3.75`

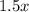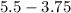
solving the subtraction on the right side

`1.5x` ≥
`1.75`

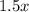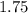
and now we move the 1.5 that multiplies to the x, to the right dividing:

`x` ≥
`1.75/1.5`

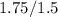
solving the division:

`x` ≥
`1.666...`

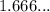
since the value 1.666667

is not an exact number, is better to leave it as a fraction:

`1.666...=(7)/(6)`

so the answer is:

`x` ≥
`(7)/(6)`

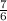
so any value equal or greater 7/6 is a solution of the inequality

Answer 2

x≥
`(7)/(6)`

Explanation:

given 1.5x+3.75≥5.5

→ 1.5x≥5.5-3.75

→ 1.5x≥1.75

→ x≥
`(1.75)/(1.5)`

→ x≥
`(7)/(6)`