Question

A uniform solid sphere has a moment of inertia I about an axis tangent to its surface. What is the moment of inertia of this sphere about an axis through its center?

a) 7/5 I
b) 3/5 I
c) 2/5 I
d) 1/7 I
e.2/7 I

Answer 1

option E

Step-by-step explanation:

given,

I is moment of inertia about an axis tangent to its surface.

moment of inertia about the center of mass

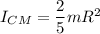`I_(CM) = (2)/(5)mR^2`.....(1)

now, moment of inertia about tangent

`I= (2)/(5)mR^2 + mR^2`

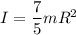`I= (7)/(5)mR^2`...........(2)

dividing equation (1)/(2)

`(I_(CM))/(I)= ((2)/(5)mR^2)/((7)/(5)mR^2)`

`(I_(CM))/(I)=(2)/(7)`

`I_(CM)=(2)/(7)I`

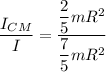
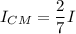
the correct answer is option E