Question

Consider the parent function f(x) = x^2 and the transformed function f(x) =- 5(x - 4)^2 – 8. Identify the

transformations.
Answer

Answer 1

Given:

The parent function is

`f(x)=x^2`

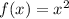
Consider the transformed function is g(x) instead of f(x) because both functions are different.

`g(x)=-5(x-4)^2-8`

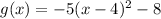
Explanation:

We have,

`f(x)=x^2`

`g(x)=-5(x-4)^2-8`

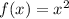
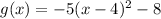
It can be written as

`g(x)=-5f(x-4)-8` ...(i)

The translation is defined as

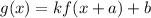`g(x)=kf(x+a)+b` .... (ii)

Where, k is stretch factor, a is horizontal shift and b is vertical shift.

If 0<|k|<1, then the graph compressed vertically by factor k and if |k|>1, then the graph stretch vertically by factor k.

If k is negative, then f(x) is reflected across the x-axis to get g(x).

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

On comparing (i) and (ii), we get

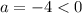`a=-4<0`, f(x) shifts 4 units right.

`b=-8<0`, f(x) shifts 8 units down.

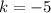`k=-5`, it is negative so f(x) reflected across the x-axis.

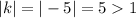`|k|=|-5|=5>1`, so f(x) stretched vertically by factor 5.

Therefore, the function f(x) reflected across the x-axis, stretched vertically by factor 5 and shifted 4 units right 8 units down to get g(x).