Question

The end point of a spring vibrates with a period of 2.1 seconds when a mass m is attached to it. When this mass is increased by 6.810×101 kg, the period is found to be 3.4 seconds. Find the value of m.

Answer 1

Mass attached to the spring is 41.95 kg

Step-by-step explanation:

We have given time period of the spring T = 2.1 sec

Let the mass attached is m

And spring constant is k

We know that time period is given by

`T=2\pi \sqrt{(m)/(k)}`

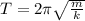
`2.1=2\pi \sqrt{(m)/(k)}`---------eqn 1

Now if the mass is increased by 68.10 kg then time period become 3.4 sec

So
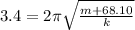`3.4=2\pi \sqrt{(m+68.10)/(k)}`------eqn 2

Now dividing eqn 1 by eqn 2

`(2.1)/(3.4)=\sqrt{(m)/(m+68.10)}`

`0.381=(m)/(m+68.10)`

`m=41.95 kg`

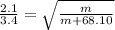
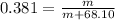
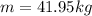
So mass attached to the spring is 41.95 kg