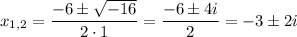Answer:
1.
a. 2.75 seconds
b. 169 feet
2. x - 3 is a factor
Other factors: x + 2, 2x + 1, 3x - 4
3. Real zeros:

Complex zeros:
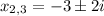
Explanation:
1. Given equation of parabola
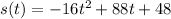
a) The rocket reaches its maximum height at the vertex of parabola. Find t-coordinate of the vertex:
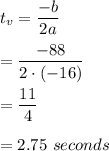
b) The maximum height is s-coordinate of the vertex. Find it:

2. For x – 3 to be a factor of
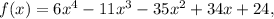 the Factor Theorem says that x = 3 must be a zero of f(x). Check it (whether f(3)=0):
the Factor Theorem says that x = 3 must be a zero of f(x). Check it (whether f(3)=0):
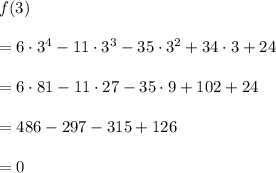
So, x = 3 is zero of the function f(x) and x - 3 is the factor of the function f(x). Rewrite the function as follows:
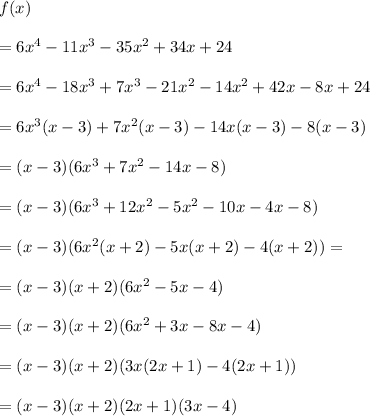
3.
 is a zero of the function
is a zero of the function
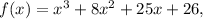 then
then
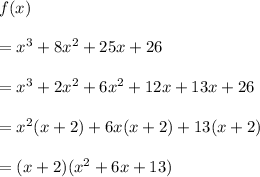
Find the discriminant of the quadratic polynomial
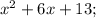
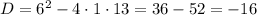
This expression has no more real zeros (the discriminant is less than 0), it has two complex zeros: