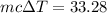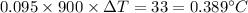Question

A 0.095-kg aluminium sphere is dropped from the roof of a 55-m-high building. The specific heat of aluminium is 900 J/kg⋅C∘ .

If 65 % of the thermal energy produced when it hits the ground is absorbed by the sphere, what is its temperature increase?

Answer 1

Increase in temperature will be
`0.389^(\circ)C`

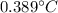
Step-by-step explanation:

We have given mass of the aluminium m = 0.095 kg

Height h = 55 m

Specific heat of aluminium c = 900 J/kg°C

We know that potential energy is given as

`PE=mgh=0.095* 9.8* 55=51.205`

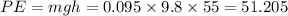
Now 65 % of potential energy
`=(51.205* 65)/(100)=33.28`

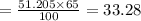
Now this energy is used to increase the temperature

So
`mc\Delta T=33.28`

`0.095* 900* \Delta T=33.28`

`0.095* 900* \Delta T=33=0.389^(\circ)C`