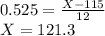Question

Membership in an elite organization requires a test score in the upper 30% range. If the mean is equal to 115 and the standard deviation is equal to 12, find the lowest acceptable score that would enable a candidate to apply for membership. Assume the variable is normally distributed. (Show Work)

Answer 1

Lowest acceptable score = 121.3

Explanation:

Mean test score (μ) = 115

Standard deviation (σ) = 12

The z-score for any given test score 'X' is defined as:

`z=(X-\mu)/(\sigma)`

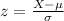
In this situation, the organization is looking for people who scored in the upper 30% range, that is, people at or above the 70-th percentile of the normally distributed scores. At the 70-th percentile, the corresponding z-score is 0.525 (obtained from a z-score table). The minimum score, X, that would enable a candidate to apply for membership is:

`0.525=(X-115)/(12)\\X=121.3`