Answer:
The graph is shown below.
The time to make the taste to half is 4.265 s.
Explanation:
Given:
Initial value of the taste is,
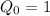
Therefore, the quality of taste over time 't' is given as:
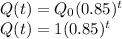
Now, when the taste reduces to half,
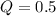
Therefore,
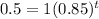
Taking natural log on both the sides, we get:
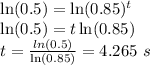
Therefore, the time to make the taste to half is 4.265 s.