Answer:
g'(10) =
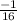
Step-by-step explanation:
Since g is the inverse of f ,
We can write
g(f(x)) = x (Identity)
Differentiating both sides of the equation we get,
g'(f(x)).f'(x) = 1
g'(10) =
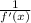 --equation[1] Where f(x) = 10
--equation[1] Where f(x) = 10
Now, we have to find x when f(x) = 10
Thus 10 =
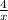 + 2
+ 2
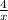 = 8
= 8
x =

Since f(x) =
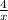 + 2
+ 2
f'(x) = -
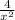
f'(
 ) = -4 × 4 = -16
) = -4 × 4 = -16
Putting it in equation 1, we get:
We get g'(10) = -
