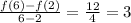Answer:
Average rate of change= 3
Explanation:
Recall the definition of average rate of change of a function
 in an interval
in an interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) :
:
Average rate of change =

In your case:
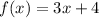 , and the interval
, and the interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) i
i
![[2,6]](https://img.qammunity.org/2020/formulas/mathematics/college/6ij163r4z33s71xldavsmyx1o7hy73wxfz.png) , therefore:
, therefore:
Average rate of change =
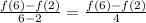
Now we evaluate the function at the two requested points:
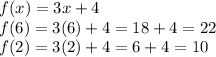 , then
, then
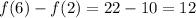
So finally the Average rate of change is: