Answer:
6.
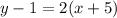
5.
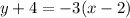
4.
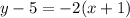
3.
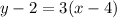
2.
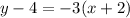
1.
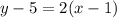
Explanation:
In the Point-Slope Formula [y - y₁ = m(x - x₁)], all the negative symbols give the OPPOSITE terms of what they really are, so be EXTREMELY CAREFUL inserting the coordinates into the formula with their CORRECT SIGNS.
I am joyous to assist you anytime.