Answer: No, this is not necessarily evidence that the proportion of Americans who are afraid to fly has increased.
Explanation:
Since we have given that
n = 1400
x = 154
So,
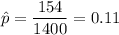
and p = 0.10
So, hypothesis would be

So, the test statistic value would be
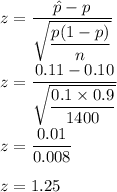
At 5% level of significance,
critical value would be 1.96.
Since 1.96>1.25.
so, we will accept the null hypothesis.
Hence, no, this is not necessarily evidence that the proportion of Americans who are afraid to fly has increased.