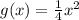Answer:
g(x) is a dilation of function f(x), and
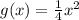
Explanation:
Function f is
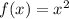
So:
When
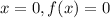
When
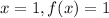
When
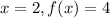
When
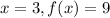
Now
For function g, looking at the graphic, we have that:
When
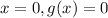
When
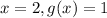
When
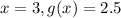
That is, g(x) is a fourth of f(x).
This means that we have a dilation by a factor of 1/4, so