Answer:
All requested products give the same answer, a = b = c = d = 3
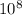 therefore type "3" in each the boxes.
therefore type "3" in each the boxes.
Explanation:
You are asked to evaluate "k" (the product between wavelength and frequency) for all cases, and write your answer in scientific notation.
Let's work on each of them:
1)
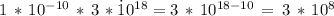 , therefore the requested value "a" (factor that multiplies
, therefore the requested value "a" (factor that multiplies
 is 3.
is 3.
2)
 , and again, the factor that multiplies
, and again, the factor that multiplies
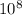 is 3.
is 3.
3)

so once more the multiplicative factor your are being ask to find is "3".
4)
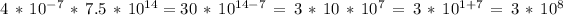 this shows that even the last product results in the same value for the factor "3" that multiplies
this shows that even the last product results in the same value for the factor "3" that multiplies
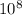 .
.
For your information, this repeated result that we are getting by making the product of the wavelength of a type of radiation and its frequency is the value of the speed of light in vacuum in km/s.