Question

A random sample of 157 recent donations at a certain blood bank reveals that 86 were type A blood. Does this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood? Carry out a test of the appropriate hypotheses using a significance level of 0.01. State the appropriate null and alternative hypotheses.

Answer 1

Answer: Yes, this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood.

Explanation:

Since we have given n = 157

x = 86

So,
`\hat{p}=(x)/(n)=(86)/(157)=0.55`

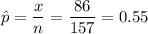
and we have p = 0.4

So, hypothesis would be

`H_0:p=\hat{p}\\\\H_a:p\\eq \hat{p}`

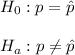
Since there is 1% level of significance.

So, test statistic value would be

`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}\\\\z=\frac{0.55-0.40}{\sqrt{(0.4* 0.6)/(157)}}\\\\z=(0.15)/(0.039)\\\\z=3.846`

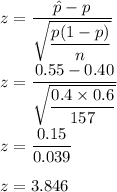
and the critical value at 1% level of significance , z = 2.58

Since 2.58<3.846.

So, we reject the null hypothesis.

Hence, Yes, this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood.