Question

A physical therapist wants to determine the difference in the proportion of men and women who participate in regular sustained physical activity. What sample size should be obtained if he wishes the estimate to be within two percentage points with 90​% ​confidence, assuming that

​(a) he uses the estimates of 21.6​% male and 19.2​% female from a previous​ year?
​(b) he does not use any prior​ estimates?

Answer 1

Using the estimates from a previous year (21.6% male and 19.2% female), a sample size of 811 should be obtained. If no prior estimates are used, a sample size of 848 is needed.

Step-by-step explanation:

To determine the sample size needed for estimating the difference in the proportion of men and women who participate in regular sustained physical activity, we can use the formula:

`n = (Z^2 * p * (1-p)) / E^2`

Where:

1. n is the required sample size
2. Z is the Z-score corresponding to the desired confidence level (90%)
3. p is the estimated proportion in the population (either the estimates from a previous year or a hypothesized value)
4. E is the desired margin of error (two percentage points)

(a) If the therapist uses the estimates of 21.6% male and 19.2% female from a previous year, we can assume that the sample proportion for both genders is the same (20.4%).

Plugging in the values:

`n = ((1.645^2) * 0.204 * (1-0.204)) / (0.02^2)`

= 810.611

Therefore, a sample size of 811 should be obtained.

(b) If the therapist does not use any prior estimates, we can assume that the sample proportion for both genders is 0.5 (maximum variability).

Plugging in the values:

`n = ((1.645^2) * 0.5 * (1-0.5)) / (0.02^2)`

= 847.075

Therefore, a sample size of 848 should be obtained.

Answer 2

Step-by-step explanation:

The standard normal distribution represents a normal curve with mean 0 and standard deviation 1. Thus, the parameters involved in a normal distribution are mean(μ) and standard deviation(σ)

The general formula for the sample size is given below:

`n=p^(')(1-p^('))(\frac{Z_{(a)/(3) } }{E} )^(2)`

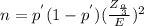
The formular for finding sample size is given as:

`n=(\frac{Z_{(a)/(3) } }{E} )^(2) * (p_(1)(1-p_(1))+p_(2)(1-p_(2)))`

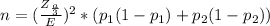
a.)

it is given that
`E=±0.02, p^(')_(1)=0.216, p^(')_(2)=0.192`

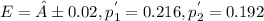
The confidence level is 0.90

For (1 - ∝) = 0.90

∝=0.10; ∝/2 = 0.05

frm the standard normal table, the required
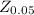`Z_(0.05)` value for 90% confidence is 1.645. The sample size is as shown:

`n=(\frac{Z_{(a)/(3) } }{E} )^(2) * (p_(1)(1-p_(1))+p_(2)(1-p_(2)))`

=
`n=((1.645)/(0.05) )^(2) * (0.216(1-0.216)+0.192(1-0.192))\\=351.22≅352`

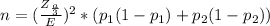
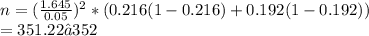
The required sample size is 352 (nearest whole number)

b.)

it is given that
`E=±0.02, p^(')_(1)=0.5, p^(')_(2)=0.5`

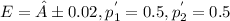
The confidence level is 0.90

For (1 - ∝) = 0.90

∝=0.10; ∝/2 = 0.05

frm the standard normal table, the required
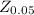`Z_(0.05)` value for 90% confidence is 1.645. The sample size is as shown:

`n=(\frac{Z_{(a)/(3) } }{E} )^(2) * (p_(1)(1-p_(1))+p_(2)(1-p_(2)))`

=
`n=((1.645)/(0.05) )^(2) * (0.5(1-0.5)+0.5(1-0.5))\\=541.205≅542`

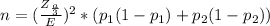
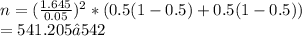
The required sample size is 542 (nearest whole number)