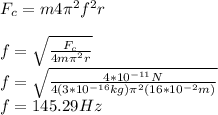Question

A sample of blood is placed in a centrifuge of radius 16.0 cm. The mass of a red blood cell is 3.0 ✕ 10−16 kg, and the magnitude of the force acting on it as it settles out of the plasma is 4.0 ✕ 10−11 N. At how many revolutions per second should the centrifuge be operated?

Answer 1

`f=145.29Hz`

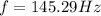
Step-by-step explanation:

The centripetal force is given by:

`F_c=ma_c(1)`

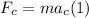
Here m is the body's mass in which the force is acting and
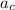`a_c` is the centripetal acceleration:

`a_c=(v^2)/(r)(2)`

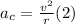
Here v is the speed of the body and r its radius. The speed is given by:

`v=2\pi fr(3)`

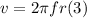
Replacing (3) in (2):

`a_c=4\pi^2f^2r(4)`

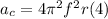
Replacing (4) in (1) and solving for f:

`F_c=m4\pi^2 f^2r\\\\f=\sqrt{(F_c)/(4m\pi^2r)}\\f=\sqrt{(4*10^(-11)N)/(4(3*10^(-16)kg)\pi^2(16*10^(-2)m))}\\f=145.29Hz`