Question

A wing with an elliptical planform is flying through sea-level air at a speed of 55 m/s. The wing is untwisted, has the same section from root to tip and its loading is W/S = 1000 N/m2 . The 2D lift curve slope is a0 = 5.7. The span of the wing is 15 m and the aspect ratio if 5. Find, a) The sectional lift coefficient. b) The sectional induced-drag coefficient. c) The effective, induced and geometric angles of attack if L=0 = -2 degrees.

Answer 1

Step-by-step explanation:

a.) To find Secrional liftSectional lift Coefficient
`(c_(I))=(W)/((0.5*Rho*V^(2)))`

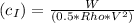
where Rho = 1.225Kg/m³ (density of air at sea level)

`(c_(I))=(1000)/((0.5*1.225*55^(2)))=0.5397`

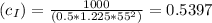
b.) To obtain the sectional induced coefficient:

`C_(D) = ((C_(L))^2)/(π(AR))`

`C_(D) = ((0.5397)^2)/(π(5))=0.0185`

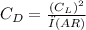
C.) For the effective angle of attack ∝0

∝0 =
`(C_(l))/(m_(0))\\=(0.5397)/(5.7)\\=0.0947rad`

For induced angle of attack ∝i:

∝i=
`(-C_(D))/(C_(L))\\=(-0.0185)/(0.5397)\\=-0.0343rad`

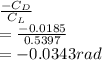
For absolute angle of attack ∝a:

∝a = ∝0 - ∝i = 0.0947 - (-0.0343) = 0.1290 rad

For geometric angle of attack ∝g:

∝g = ∝a + ∝L given ∝L = -2°≅-0.0349 rad

= 0.1290-0.0349 = 0.0941rad