Answer:
We conclude that the mean number of residents in the retirement community household is less than 3.36 persons.
Explanation:
We are given the following in the question:
Population mean, μ = 3.36
Sample mean,
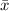 = 2.71
= 2.71
Sample size, n = 25
Alpha, α = 0.10
Sample standard deviation, s = 1.10
First, we design the null and the alternate hypothesis
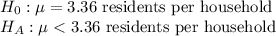
We use One-tailed(left) t test to perform this hypothesis.
Formula:
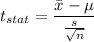 Putting all the values, we have
Putting all the values, we have
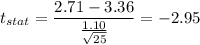
Now,
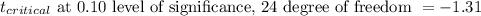
Since,
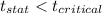
We reject the null hypothesis and fail to accept it.
Thus, we conclude that the mean number of residents in the retirement community household is less than 3.36 persons.