Question

We​ don't know f (x) but we do know that x = 1 is a critical number of f' (x) and we know f" (x)=12x. Use this information to decide if​ f(x) has a relative minimum or maximum at x=1.

Answer 1

relative minimum

Explanation:

From f^''(x) = 12x we can take the integration to find out what f'(x) is:

`f'(x) = 6x^2 + C`

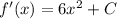
Furthermore, we can substitute x = 1 for f''(x) to find out whether it's positive or negative

f''(1) = 12*1 = 12 > 0

So if x=1 is a critical point of f'(x) and f''(x=1) > 0 then that point is a relative minimum point