Question

An oil refinery is located on the north bank of a straight river that is 2 km wide. A pipeline is to be constructed from the refinery to storage tanks located on the south bank of the river 3 km east of the refinery. The cost of laying pipe is $400,000 per km over land to a point P on the north bank and $800,000 per km under the river to the tanks. To minimize the cost of the pipeline, how far from the refinery should P be located? (Round your answer to two decimal places.)

Answer 1

P is exactly 3km east from the oil refinery.

Explanation:

Let's d be the distance in km from the oil refinery to point P. So the horizontal distance from P to the storage is 3 - d and the vertical distance is 2. Hence the diagonal distance is:

`√((3 - d)^2 + 2^2) = √((3 - d)^2 + 4)`

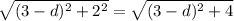
So the cost of laying pipe under water with this distance is

`800000√((3 - d)^2 + 4)`

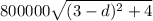
And the cost of laying pipe over land from the refinery to point P is 400000d. Hence the total cost:

`800000√((3 - d)^2 + 4) + 400000d`

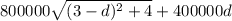
We can find the minimum value of this by taking the 1st derivative and set it to 0

`800000(2*0.5*(3-d)(-1))/(√((3 - d)^2 + 4)) + 400000 = 0`

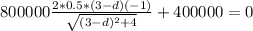
We can move the first term over to the right hand side and divide both sides by 400000

`1 = 2(3 - d)/(√((3 - d)^2 + 4))`

`√((3 - d)^2 + 4) = 6 - 2d`

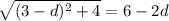
From here we can square up both sides

`(3 - d)^2 + 4 = (6 - 2d)^2`

`9 - 6d + d^2 + 4 = 36 - 24d + 4d^2`

`3d^2-18d+27 = 0`

`d^2 - 6d + 9 = 0`

`(d - 3)^2 = 0`

`d -3 = 0`

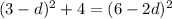
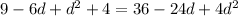
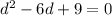
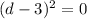
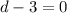
d = 3

So the cost of pipeline is minimum when P is exactly 3km east from the oil refinery.